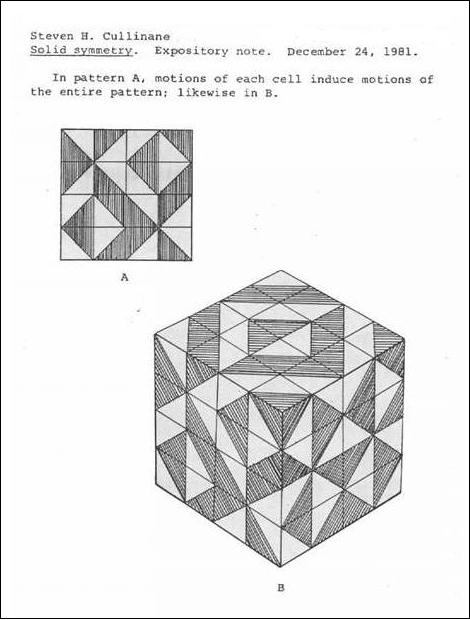
|
Josefine Lyche
Born in 1973 in Bergen, Norway.
Lives and works in Oslo and Berlin.
Keywords (to help place my artwork in the
proper context): Aliens, affine geometry, affine
planes, affine spaces, automorphisms, binary
codes, block designs, classical groups, codes,
coding theory, collineations, combinatorial,
combinatorics, conjugacy classes, the Conwell
correspondence, correlations, Cullinane,
R. T. Curtis, design theory, the diamond theorem,
diamond theory, duads, duality, error correcting
codes, esoteric, exceptional groups,
extraterrestrials, finite fields, finite geometry, finite
groups, finite rings, Galois fields, generalized
quadrangles, generators, geometry, GF(2),
GF(4), the (24,12) Golay code, group actions,
group theory, Hadamard matrices, hypercube,
hyperplanes, hyperspace, incidence structures,
invariance, Karnaugh maps, Kirkman’s schoolgirls
problem, Latin squares, Leech lattice, linear
groups, linear spaces, linear transformations,
Magick, Mathieu groups, matrix theory, Meno,
Miracle Octad Generator, MOG, multiply transitive
groups, occultism, octahedron, the octahedral
group, Orsic, orthogonal arrays, outer automorphisms,
parallelisms, partial geometries,
permutation groups, PG(3,2), Plato, Platonic
solids, polarities, Polya-Burnside theorem, projective
geometry, projective planes, projective
spaces, projectivities, Pythagoras, reincarnation,
Reed-Muller codes, the relativity problem,
reverse engineering, sacred geometry, Singer
cycle, skew lines, Socrates, sporadic simple
groups, Steiner systems, Sylvester, symmetric,
symmetry, symplectic, synthemes, synthematic,
Theosophical Society tesseract, Tessla, transvections,
Venn diagrams, Vril society, Walsh
functions, Witt designs.
(See also the original catalog page.)
|






















































 .
.

















.gif)
















 .
.